2.6 Comparisons, Vector Subsetting & Change Values
By now, you are more than familiar with the simplest type of R objects—vector, and you can create vectors and apply many useful functions on vectors. Sometimes you may be wondering how to extract certain elements from a vector? In this section, we will introduce some new operations on vectors that can help you get the desired subvector.
2.6.1 Comparisons on vectors of the same type
The first type of operations we want to introduce is making comparisons between two vectors of the same type. Similar to the arithmetic operations between two numeric vectors in Section 2.1, we normally want to compare two vectors of the same length, but we can also compare two vectors of different lengths according to the recycling rule in R.
a. Compare two vectors of the same length
If two vectors are of the same length, the comparison is done elementwisely, just like the arithmetic operations in Section 2.1.
Let’s take numeric vectors for example. You can create a numeric vector x with value 3, and compare it to another numeric vector 2 to find out whether the value of x is smaller than 2 or not.
x <- 3
x < 2
#> [1] FALSESince 3 is bigger than 2, you will certainly get FALSE!
In addition to the less than sign <, there are a few other commonly useful operators for doing comparisons.
x < 2 #less
x <= 2 #less or equal to
x > 1 #bigger
x >= 1 #bigger or equal to
x == 3 #equal to
#x = 3 #assignment operator
x != 3 #not equal toNote that if you want to check whether two vectors are equal, you have to use two equal signs as a single operator, which is ==, to do comparisons. If only one equal sign is used, it would work like an assignment operator. In addition, you can use an exclamation mark together with a equal sign, which is !=, to find out whether two vectors are not equal.
Note that as we explained in Section 1.3.2, sometimes you need to execute an R expression because you can get its object type and value from the result. Here, you may notice that you get TRUE or FALSE as the result from the codes above. Since TRUE and FALSE are logical values (there are no pairs of double quotes around TRUE’s and FALSE’s when you use them as logical values), you know that all comparison operations generate logical vectors. Of course, you can assign the result to a name for future use. Let’s take x > 1 for example.
class(x > 1)
length(x > 1)
big1 <- x > 1
big1
class(big1)So x > 1 and big1 are both logical vectors with length one.
Also, you can create two length>1 numeric vectors y and z with the same length, then do comparisons between them.
y <- c(3,5,7,5,3)
z <- c(2,6,7,6,3)
y > z
#> [1] TRUE FALSE FALSE FALSE FALSEFrom the result, you can see that y > z is a length-5 logical vector. The values of y > z are obtained by making elementwise comparisons between the corresponding elements in these two vectors.
big2 <- y > z
big2
class(big2)
which(big2)By assigning y > z to a big2, you create another logical vector. Here, the which() function returns the locations of all TRUE values, so you will get a result of 1 for big2.
You can also compare two character vectors, which works by comparing the corresponding strings in the same location. The rule for comparison is the alphabetically order explained in Section 2.4.2. Similar to comparing numerical vectors, we also use two equal signs == to check whether the corresponding elements in the two input vectors have the same value. Let’s first create two character vectors with the same length, then use == to compare them. Since the expression of this comparison is again a logical vector, you can create a new logical vector same1 and get the locations of TRUE values. You can also use other comparison operators.
animals <- c("pig", "monkey", "pig")
zoo <- c("sheep", "monkey", "pig")
same1 <- animals == zoo
which(same1)
which(animals != zoo)Comparisons between logical vectors work similarly as character vectors, where we usually use == or != to compare corresponding elements in logical vectors. Here are some examples.
logi1 <- c(TRUE, FALSE, FALSE)
logi2 <- c(TRUE, TRUE, TRUE)
same2 <- logi1 == logi2
which(same2)
which(logi1 != logi2)b. Compare between one vector with length > 1 and another vector with length 1
The recycling rule also works for the comparison operations in R. With an vector of length 1, you can compare the value of it to the values of another vector with more than one elements one by one, which generates a logical vector. The length of the logical vector will be the same as that of the longer vector. Here are some examples.
y != x
animals == "pig"
logi1 == TRUE2.6.2 Comparisons on vectors of different types
When you try to compare two vectors of different types, the coercion rule in Section 2.2.3 will apply. In particular, values of corresponding elements will be unified into the more complex one when making comparisons between two vectors. The order of complexity from simple to complex is still \(\mbox{logical} < \mbox{integer} < \mbox{double} < \mbox{character}\). Let’s try to compare between a numeric vector and a logical vector,
a <- c(-1, 0, 1)
b <- c(TRUE, FALSE, TRUE)
a == b
#> [1] FALSE TRUE TRUEThen you will get a length-3 logical vector. In a == b, the first element is obtained by using == to compare -1 and TRUE, then R will convert TRUE to 1 and make comparison between -1 and 1 since numbers are more complex than logical values. The second and third elements are also obtained in a similar fashion. This is the most common use of comparisons between vectors of different types.
You can make comparisons between vectors of other types, the following example shows that the classic transitive property in math (\(a=b\) and \(b=c\) imply \(a=c\)) doesn’t hold in R.
1 == TRUE
#> [1] TRUE
TRUE == "TRUE"
#> [1] TRUE
1 == "TRUE"
#> [1] FALSE2.6.3 Vector subsetting
Sometimes you may want to extract particular elements from a vector, then the extracted elements will constitute a new vector, which is a subvector of the original vector. This process is called vector subsetting, and the subvector will be of the same type as the original one.
In this part, we will introduce two common ways to do vector subsetting in R. Before we get started, let’s create a vector which will be used throughout this part.
h <- c(3,1,4,2,90)a. Use logical vectors to do vector subsetting
Firstly, we introduce how to use logical vectors to do vector subsettings. You need to use a pair of square brackets [ ] after a vector, then put a logical vector of the same length as the original vector inside the square brackets. Here is an example,
h[c(TRUE, FALSE, TRUE, FALSE, TRUE)]
#> [1] 3 4 90From the result, you can see that the values from h with the same positions of TRUEs are extracted. Since 3, 4 and 90 are parts of the values of h, the vector composed of 3 4 90 is a subvector of h. When assigning these three values to a name, you will get a named subvector sub1.
sub1 <- h[c(TRUE, FALSE, TRUE, FALSE, TRUE)]
sub1
#> [1] 3 4 90In addition to writing the logical vector in an explicit form, you can also use a named logical vector or an expression whose result is a logical vector. Let’s say we want to find the subvector of h for all elements in h that are larger than 2. Then, you can first compare h with 2, getting a logical vector.
big3 <- h > 2
big3
#> [1] TRUE FALSE TRUE FALSE TRUEThen you may notice that both big3 and h > 2 are identical to c(TRUE, FALSE, TRUE, FALSE, TRUE). So naturally you can also put big3 or h > 2 into [ ], which generates the same subvector with 3 4 90 as values.
h[c(TRUE, FALSE, TRUE, FALSE, TRUE)]
h[big3]
h[h > 2]If you create a character vector home and compare it to "pig", you will get another logical vector same3. Let’s try to use same3 to do vector subsetting on h.
home <- c("pig", "monkey", "pig", "monkey", "pig")
same3 <- home == "pig"
sub2 <- h[same3]
sub2
#> [1] 3 4 90Awesome! You still get the result of 3 4 90! As a result, as long as the logical vectors you use have the same values, you will get the same result after doing vector subsetting.
Of course, you can do vector subsetting on character vectors or logical vectors. Keep in mind that the result will be the same type as the original one. Try the following code by yourself.
home[same3]
home[big3]
lg <- c(TRUE, FALSE, FALSE, FALSE, TRUE)
lg[same3]
lg[big3]b. Use indices to do vector subsetting
Next, we will introduce how to use indices to do vector subsetting. To achieve this goal, you need to put a numeric vector inside [ ], for example,
h[c(2,4)] #return values of the 2nd and 4th elements of h
#> [1] 1 2You get values of the 2nd and 4th elements in h. If you add a minus sign - before the numeric vector, you will get all elements except the 2nd and 4th ones in h.
h[-c(2,4)] #return values except the 2nd and 4th elements of h
#> [1] 3 4 90Similar to using a named logical vectors, you can also use a named numeric vector to do vector subsetting.
indices <- c(2,4)
sub3 <- h[indices]
sub3Also, you can get subvectors of character vectors or logical vectors using indices.
home[indices]
lg[indices]In conclusion, there are two ways to get a subvector of h with values bigger than 2.
h <- c(3,1,4,2,90)
h[h > 2] #h > 2 will return TRUE if the element in h has value bigger than 2
h[c(1,3,5)] #It's clear to see that the first, third and fifth elements have values bigger than 2c. using names to do vector subsetting
For a named vector, we can also use character vector consisting of the names as indices to do vector subsetting.
x_w_name <- c(height = 165, weight = 60, BMI = 22)
x_w_name["height"]
#> height
#> 165
x_w_name[c("weight", "BMI")]
#> weight BMI
#> 60 222.6.4 Update values in sub-vectors
In Section 2.1.1, we have learned how to update one element in a vector using the assignment operator. For example, x[ind] <- new_value will update the ind-th element of x to the new_value. It turns out we can update the values of multiple elements of a vector in a similarly way.
a. Change all values in subsets of vectors
Firstly, let’s review values of vector h and get a subset of it.
h <- c(3,1,4,2,90)
h[c(2,4)]Obviously, you will get a numeric vector with 1 and 2 as the values. Let’s see how to change values just for a subset of h, which is actually a very important usage of doing vector subsetting. You just need to assign new values to the subset, then you can verify the values of h. Let’s see an example,
h[c(2,4)] <- c(10, 20)
h
#> [1] 3 10 4 20 90
h[c(2,4)] <- 10 #recycling rule applies
h
#> [1] 3 10 4 10 90From the result, you can see that only 1 and 2 have been changed to 10, which means you have successfully change parts of h!
b. Define the vector again
Another way to change values in vectors is to do object assignment again using the same name, then you can change any values of it.
Let’s first reset the values of h.
h <- c(3,1,4,2,90)In Section 1.3, you have learned about checking all the named objects and their values in the environment. So let’s review values of vector h from this panel together.

Figure 2.3: Values of h (1)
Now we all know that h is a numeric vector with 5 values. Then let’s try to do an object assignment again, this time you can assign different values to h and see what will happen to h.
h <- c(1,2,3,4,5)
h
#> [1] 1 2 3 4 5Then you can see that the values of h have been changed to the new ones! Another easier way to verify values of h is from the environment, so it is a good habit to monitor the environment from time to time to make sure everything look fine.

Figure 2.4: Values of h (2)
You can assign any values to h as you want, then h may change the vector type or even the object type according to the values assigned. By running the following code, h will be a character vector with three strings.
h <- c("pig", "monkey", "panda")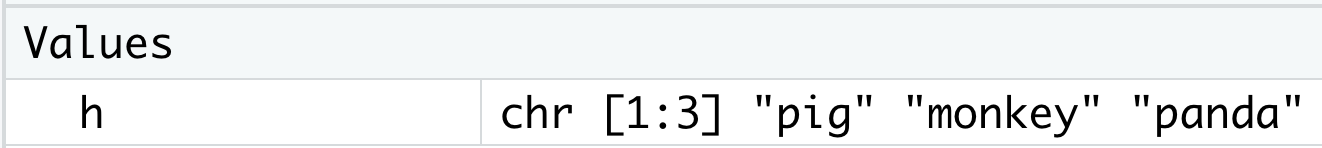
Figure 2.5: Values of h (3)
If you assign values of a subvector to a name, you will create a new named vector. Now hs is not the subset of h, it is a vector with the same value as the subset. If you assign different value(s) to hs, there will be no change on h.
h <- c(3,1,4,2,90)
hs <- h[c(2,4)]
hs <- 10
h2.6.5 Exercises
Consider the vector v1 <- c(7, 2, 4, 9, 7), v2 <- c(6, 2, 8, 7, 9), and v3 <- 1:50.
Find the locations in
v1where the corresponding value is smaller thanv2.Find the subvector of
v2such that the corresponding location inv1is larger than 5.Find the subvector of
v3such that it is divisible by 7. (Hint: the result of7%%7is equal to 0 since 7 is divisible by 7)For all elements of
v3that is divisible by 8, replace it by 100.