10.4 Multivariate Normal Distribution

In this section, we introduce how to work with multivariate normal distribution in R.

First, let’s review the definition of a multivariate normal distribution. Suppose a \(p\)-dimensional random vector \({\bf x} \sim N({\bf \mu}, {\bf \Sigma})\), where \({\bf \mu}\) is the mean vector and \({\bf \Sigma}\) is the covariance matrix. We have \[ f({\bf x}) = \frac{1}{(2\pi)^{p/2}\sqrt{|{\bf \Sigma}|}}\exp\left[-\frac{1}{2}({\bf x}-{\bf\mu})^T{\bf \Sigma}^{-1}({\bf x}-{\bf\mu})\right]. \]

10.4.1 Generate Multivate Normal Distribution

To randomly generate \({\bf x} \sim N({\bf \mu}, {\bf \Sigma})\), you can use the mvrnorm(n = 1, mu, Sigma) function in the MASS package, which is pre-loaded in the base R. The function mvnorm() takes three arguments.

  • n: targeted sample size
  • mu: mean vector
  • Sigma: covariance matrix

Let’s take a look at an example where the distribution is \(\bf\mu = (1, 2)^T\) and \[{\bf \Sigma} = \left[\begin{matrix} 1&0.8\\ 0.8&1 \end{matrix}\right]\]

library(MASS)
#> 
#> Attaching package: 'MASS'
#> The following object is masked from 'package:plotly':
#> 
#>     select
#> The following object is masked from 'package:dplyr':
#> 
#>     select
set.seed(87)
n <- 1000
mu <- c(1, 2)
Sigma <- matrix(c(1, 0.8, 0.8, 1), 2, 2)
x <- mvrnorm(n, mu, Sigma)
head(x)
#>              [,1]        [,2]
#> [1,] -1.002876112 -0.06259489
#> [2,] -0.843956459  0.57515106
#> [3,] -0.158140872 -0.39338951
#> [4,] -0.004390677  1.26823724
#> [5,]  2.483115985  3.99971514
#> [6,]  0.526159176  2.27572849

x contains \(n=1,000\) two-dimensional normal distributed variable, where each row represents one observation. Let’s try to visualize the data using a scatterplot.

normal_data <- as.data.frame(x)
colnames(normal_data) <- c("X1", "X2")

library(ggplot2)
# Visualize using ggplot
ggplot(normal_data, aes(x = X1, y = X2)) + geom_point(color = "blue", alpha = 0.6) +
    labs(title = "Scatterplot of Multivariate Normal Data", x = "X1", y = "X2") +
    theme_minimal()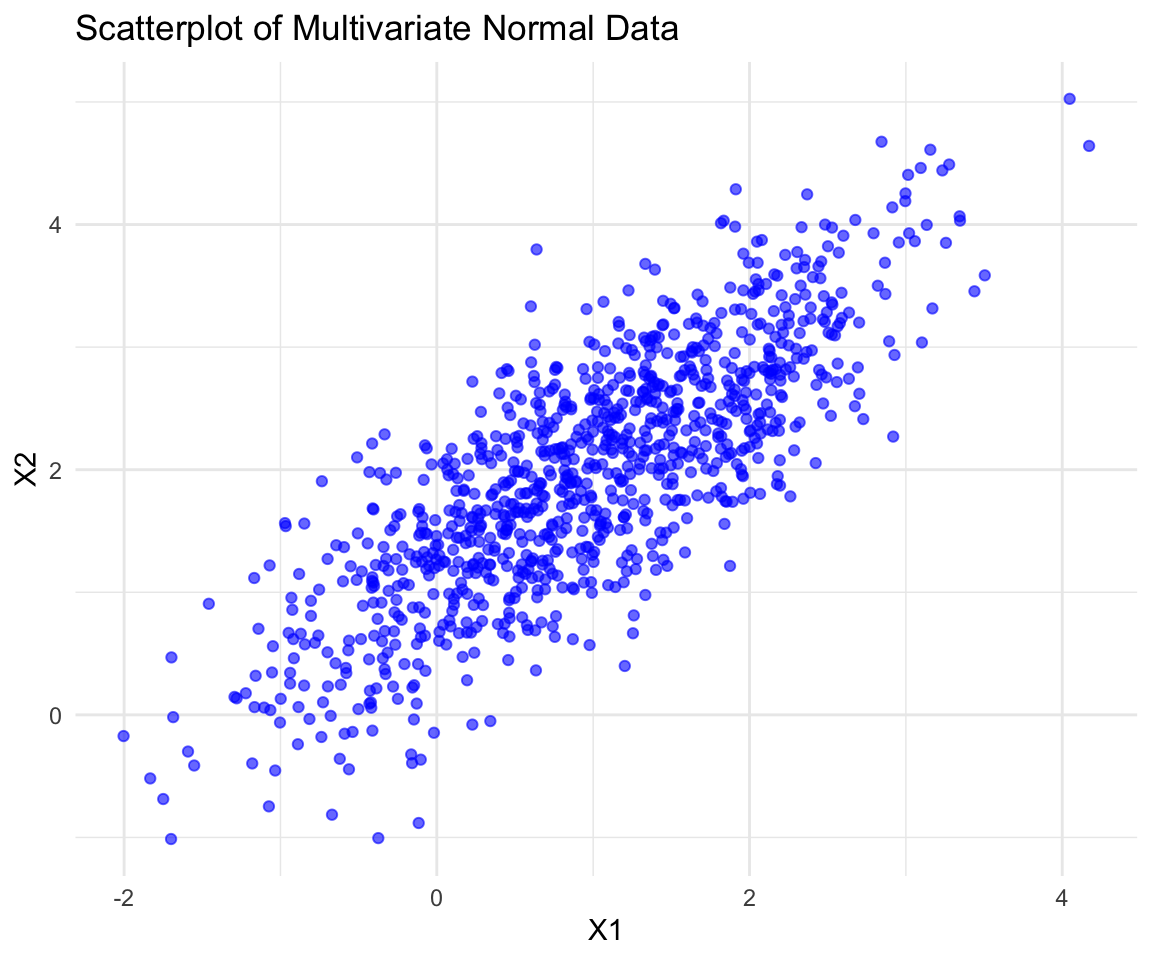

10.4.2 Properties of Multivariate Normal Distribution

  1. Marginal Distributions:
    • Each component of \({\bf x}\) follows a univariate normal distribution.
  2. Linear Combinations:
    • Any linear combination of the components of \({\bf x}\) is also normally distributed.
  3. Independence:
    • Two components of \({\bf x}\) are independent if and only if their covariance is zero.

Let’s use visualizations to verify the properties of the multivariate normal distribution.

# Marginals visualization using ggplot
ggplot(normal_data, aes(x = X1)) + geom_histogram(bins = 30, fill = "lightblue",
    color = "black", alpha = 0.7) + labs(title = "Histogram of X1", x = "X1", y = "Frequency") +
    theme_minimal()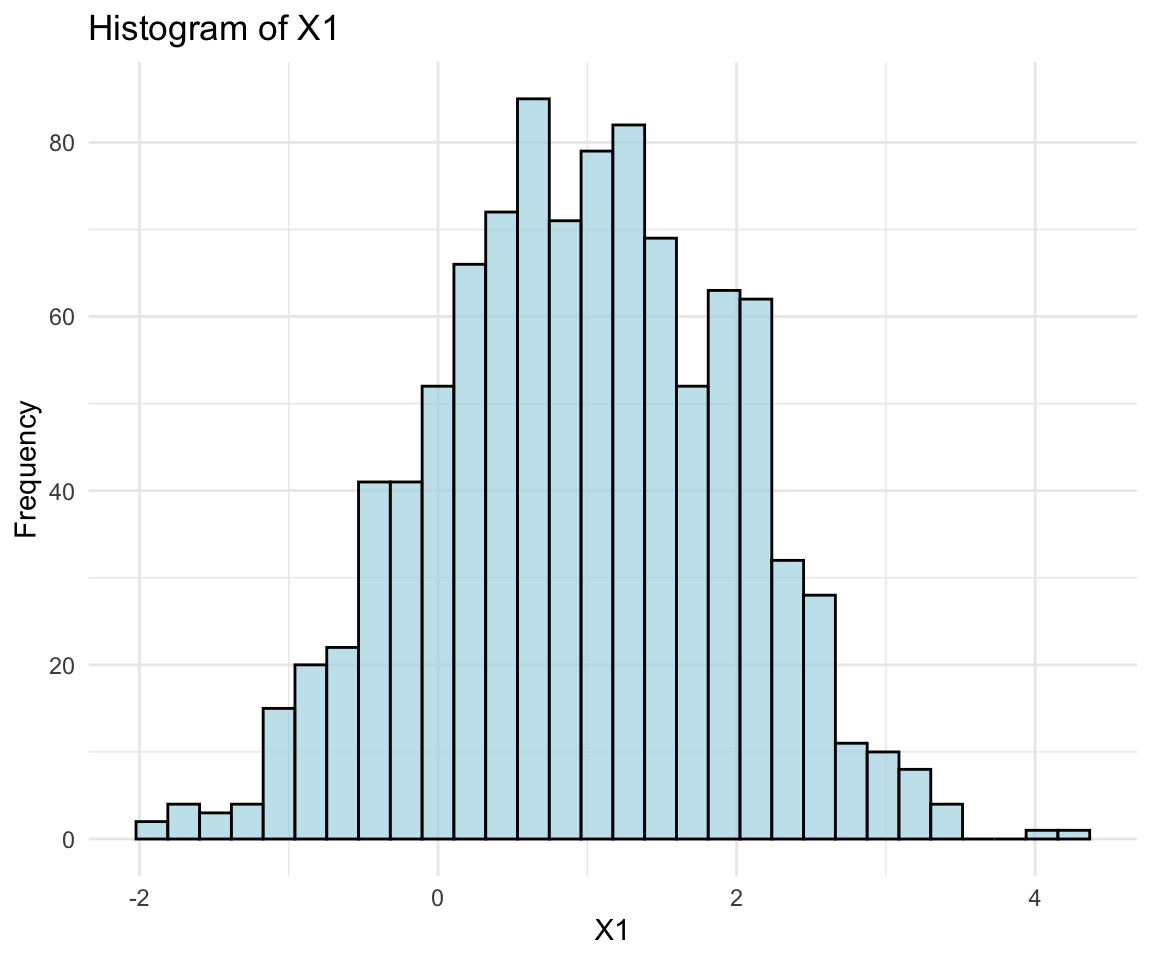


ggplot(normal_data, aes(x = X2)) + geom_histogram(bins = 30, fill = "lightgreen",
    color = "black", alpha = 0.7) + labs(title = "Histogram of X2", x = "X2", y = "Frequency") +
    theme_minimal()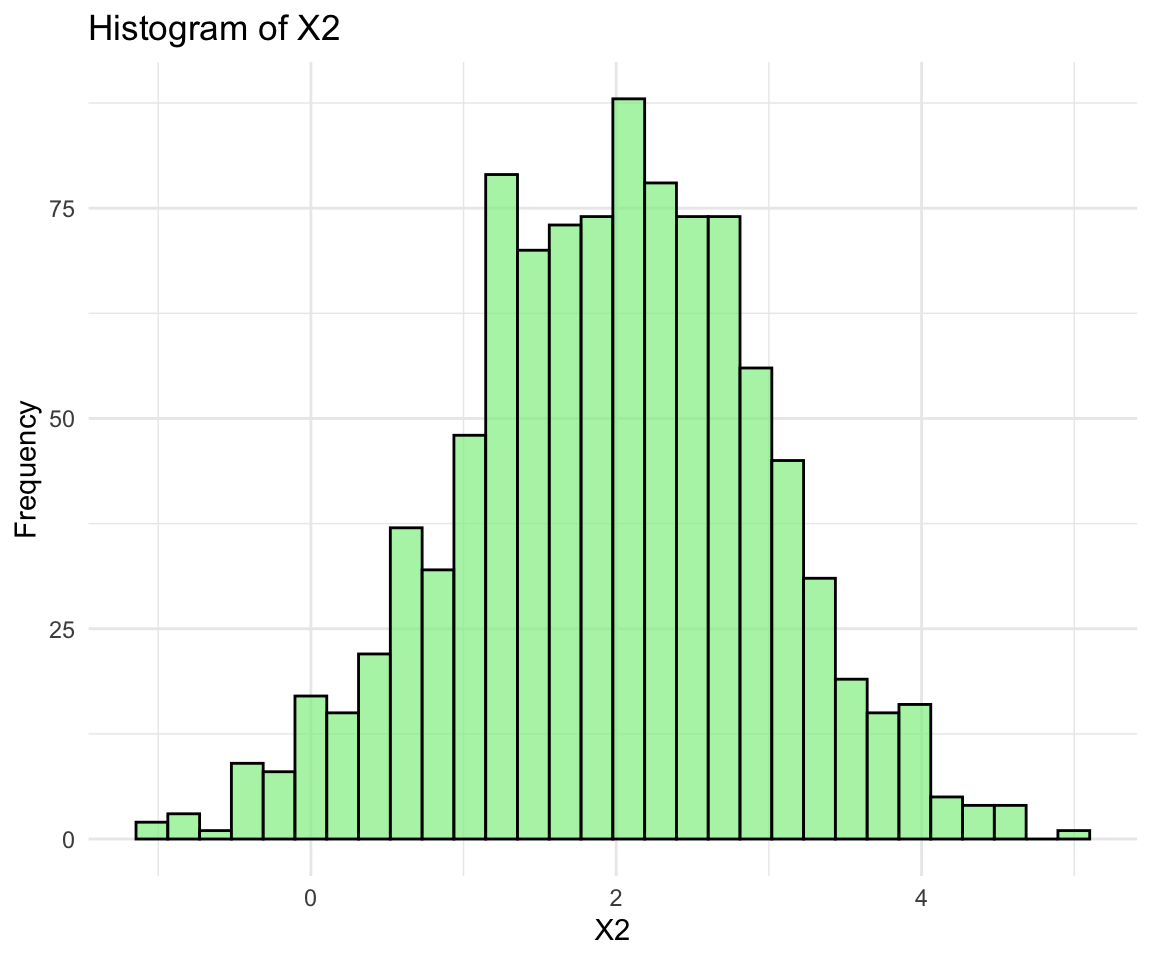


# Linear combination visualization
linear_combination <- 0.5 * normal_data$X1 + 0.5 * normal_data$X2
ggplot(data.frame(LinearCombination = linear_combination), aes(x = LinearCombination)) +
    geom_histogram(bins = 30, fill = "pink", color = "black", alpha = 0.7) + labs(title = "Histogram of Linear Combination",
    x = "Linear Combination", y = "Frequency") + theme_minimal()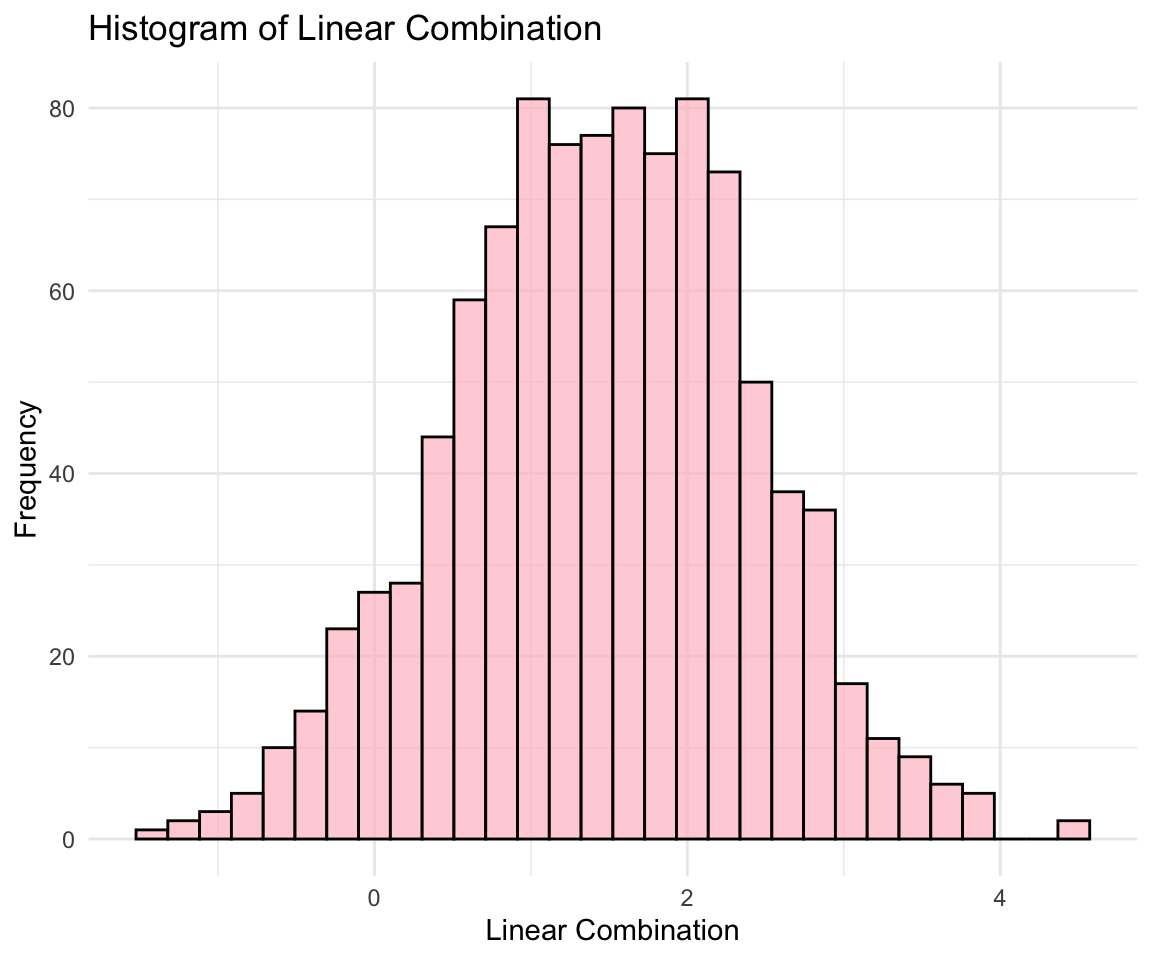

10.4.3 Sample Mean and Sample Covariance Matrix

In practical applications, we usually have a set of observations and would like to get a sample estimate of the parameters \({\bf \mu}\) and \({\bf \Sigma}\).

For the \({\bf \mu}\), you can directly use the sample mean as the estimate which is unbiased. \[\hat {\bf\mu} = [\hat\mu_j],\] where \[\hat\mu_j = \frac{1}{n}\sum_{i=1}^nx_{ij}.\]

mu_hat <- apply(x, 2, mean)
mu_hat
#> [1] 0.9528617 1.9671994

To estimate \({\bf\Sigma}\), we will use the sample covariance matrix estimate: \[\hat{\bf \Sigma} = [\hat\Sigma_{jk}],\] where \[\hat\Sigma_{jk} = \frac{1}{n-1}\sum_{i=1}^n(x_{ij}-\hat\mu_j)(x_{ik}-\hat\mu_k).\]

To compute this matrix, we can use the function cov() on the matrix x.

sigma_hat <- cov(x)
sigma_hat
#>           [,1]      [,2]
#> [1,] 1.0042256 0.8036966
#> [2,] 0.8036966 0.9964596
1/(n - 1) * sum((x[, 1] - mu_hat[1]) * (x[, 2] - mu_hat[2]))  #compute \hat\Sigma_{12} by formula
#> [1] 0.8036966

For cov() function, in addition to computing the sample covariance matrix, you can also use it to compute the covariance among two vectors \(y\) and \(z\). \[cov(y, z) = \frac{1}{n-1}\sum_{i=1}^n(y_{i}-\bar y)(z_i-\bar z).\]

Let’s try to compute the covariance between the first and second column of \(x\).

cov(x[, 1], x[, 2])
#> [1] 0.8036966
cov(x)[1, 2]
#> [1] 0.8036966

You can see that this is exactly the same as \(\hat\Sigma_{12}\).

10.4.4 Sample Correlation Matrix

Another useful measure is the sample correlation matrix. It is defined as \[\widehat{corr}(x) = [\widehat{corr}(x)_{jk}],\] where \[\widehat{corr}(x)_{jk} = \frac{\hat\Sigma_{jk}} {\sqrt{\hat\Sigma_{jj}\hat\Sigma_{kk}}}. \]

You can use cor() on the matrix x to get its sample correlation matrix.

cor(x)
#>           [,1]      [,2]
#> [1,] 1.0000000 0.8034274
#> [2,] 0.8034274 1.0000000
sigma_hat[1, 2]/sqrt(sigma_hat[1, 1] * sigma_hat[2, 2])  #verify the [1,2] element
#> [1] 0.8034274

Similar to the cov() function, you can also us the cor() function to compute the sample correlation between two vectors.

cor(x[, 1], x[, 2])
#> [1] 0.8034274
cor(x)[1, 2]
#> [1] 0.8034274

You can see that the sample correlation matrix include all the pairwise sample correlations between any of the two columns.

10.4.5 Exercise

  1. Generate 500 observations from a bivariate normal distribution with:
    • Mean vector \({\bf \mu} = (3, 5)^T\)
    • Covariance matrix \({\bf \Sigma} = \begin{bmatrix} 2 & 0.5 \\ 0.5 & 1 \end{bmatrix}\).
    • Visualize the data using a scatterplot with ggplot2.
  2. For the above data:
    • Plot the histograms of each marginal distribution using ggplot2.
    • Compute and interpret the covariance and correlation.
  3. Generate 1000 observations from a 3-dimensional normal distribution with:
    • \({\bf \mu} = (1, -1, 3)^T\)
    • \({\bf \Sigma} = \begin{bmatrix} 1 & 0.3 & 0.2 \\ 0.3 & 1 & 0.4 \\ 0.2 & 0.4 & 1 \end{bmatrix}\).
    • Compute the pairwise sample correlations between dimensions.